A unique presentation and geometrical meaning of the zeros of a quadratic polynomial | Part - 2

Geometrical Meaning of the Zeroes of a Quadratic Polynomial

For any quadratic polynomial of the form P(x) = ax² + bx + c, where a ≠ 0, the graph is a parabola. This parabola can open in one of two directions:

• Upward (when a > 0)
• Downward (when a < 0)

The locations where the graph crosses the x-axis indicate the roots or zeroes of the quadratic polynomial.

Case I: Two Distinct Real Zeroes

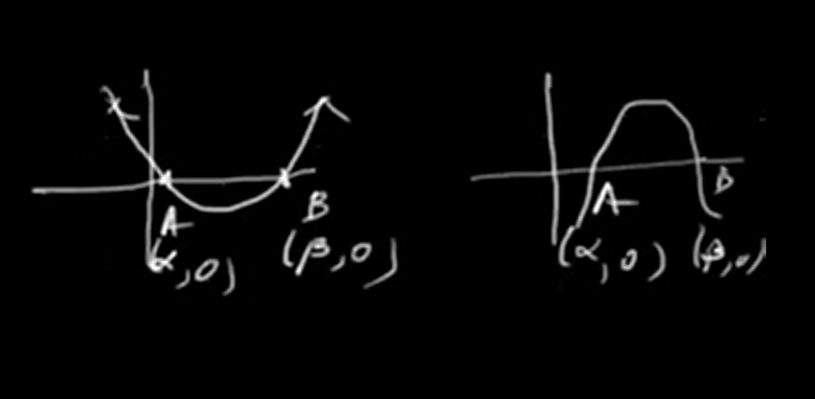
In this case, the parabola intersects the x-axis at two distinct points, say A(α, 0) and B(β, 0).

The values α and β are the zeroes of the quadratic polynomial. Therefore, the polynomial can be written as:

P(x) = k(x - α)(x - β)

In this expression, k represents a real constant that is not equal to zero.

Case II: One Real and Repeated Zero

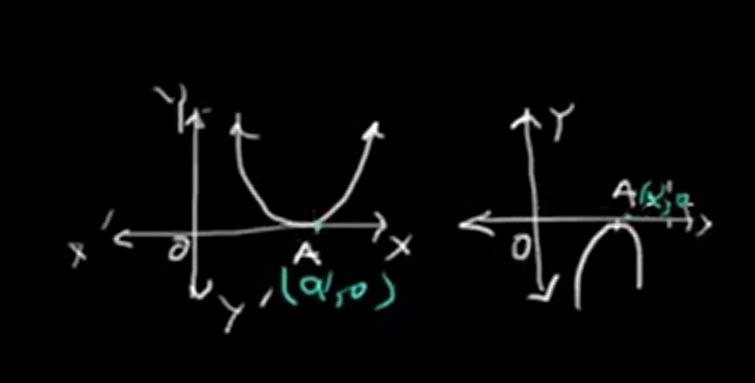
In this case, the graph makes contact with the x-axis at a single point, A(α, 0), without passing through it.

This means the polynomial has one real zero with multiplicity two, i.e., both zeroes are equal.

The polynomial in this case can be written as:

P(x) = k(x - α)²

Once again, k denotes a real number that is not equal to zero.

Case III: No Real Zeroes

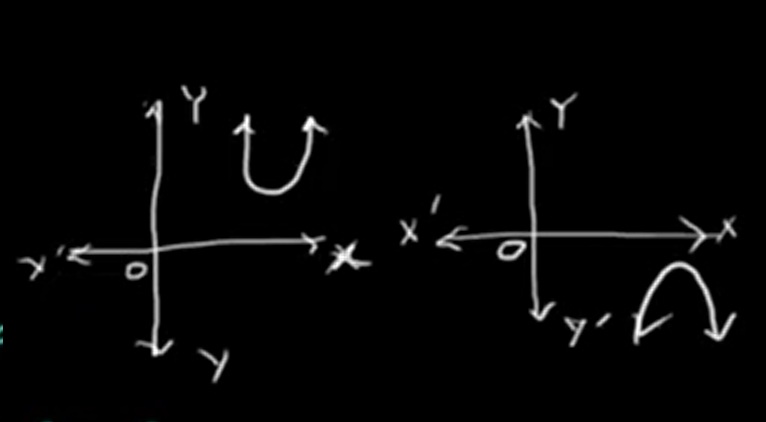
If the parabola lies entirely above or entirely below the x-axis, it means that the graph does not intersect or touch the x-axis at any point.

In this case, the quadratic polynomial has no real zeroes.

Summary

• Case I: Two distinct real zeroes — graph intersects the x-axis at two points.
• Case II: One real zero — graph touches the x-axis at a single point.
• Case III: No real zeroes — graph does not intersect the x-axis at all.