Associated angles | Introduction

Associated Angles and Their Trigonometric Signs in Different Quadrants

The sign of any trigonometric function depends on the quadrant in which the terminal side of the angle is located. Grasping this concept is important when working with angles beyond 90° and helps in simplifying trigonometric expressions using reference (associated) angles.

What Are Associated Angles?

Reference angles, also referred to as associated angles, are acute angles formed between the terminal side of a given angle and the x-axis. These angles help simplify trigonometric calculations by reducing complex angles to their corresponding values in the first quadrant.

Signs of Trigonometric Functions in Quadrants

In trigonometry, the sign of a trigonometric function is determined by the quadrant where the terminal side of the angle falls. The unit circle serves as a helpful tool to visualize and understand these sign conventions.

• First Quadrant (0° to 90°): All six trigonometric functions—sine, cosine, tangent, cosecant, secant, and cotangent—are positive.
• Second Quadrant (90° to 180°): Only sine and its reciprocal cosecant are positive; the rest are negative.
• Third Quadrant (180° to 270°): Tangent and cotangent are positive; sine, cosine, and their reciprocals are negative.
• Fourth Quadrant (270° to 360°): Cosine and secant are positive; the other functions are negative.

Mnemonic to Remember

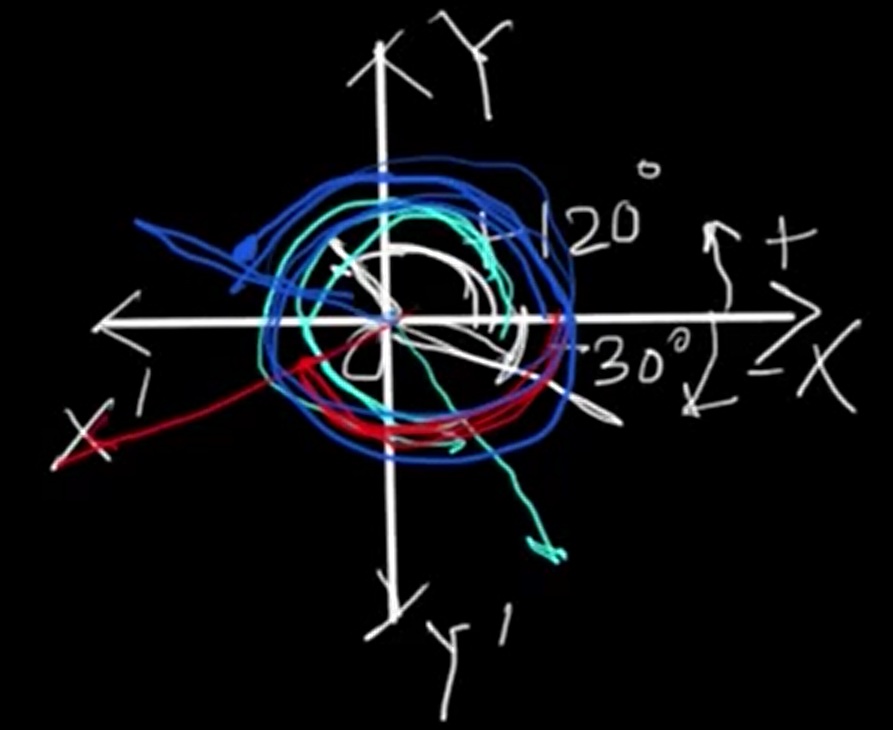
A helpful way to recall which trigonometric functions are positive in each quadrant is by using the phrase: “All Students Take Calculus.”

• All – All functions positive in the 1st quadrant
• Students – In the second quadrant, sine and its reciprocal, cosecant, have positive values
• Take – Tangent and cotangent positive in the 3rd quadrant
• Calculus – Cosine and secant positive in the 4th quadrant

Using Associated Angles

When solving trigonometric problems, we often express angles outside the first quadrant in terms of their associated angles. For example:

• sin(150°) = sin(180° - 30°) = sin(30°)
• cos(210°) = cos(180° + 30°) = -cos(30°)
• tan(330°) = tan(360° - 30°) = -tan(30°)

For every case, the angle's value is expressed in terms of a reference angle, while the sign is assigned based on the quadrant it falls in.