Distance between two points whose coordinates are given

Derivation of Distance Between Two Points Using Perpendiculars

Consider two points in a Cartesian plane:

• P(x₁, y₁)
• Q(x₂, y₂)

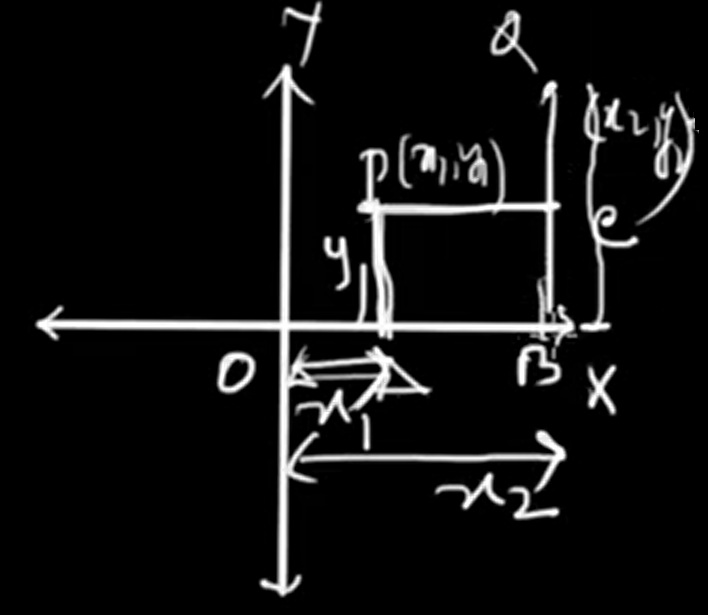
Let O represent the origin at (0, 0). From points P and Q, draw perpendicular lines down to the x-axis.

• PA is perpendicular from P to x-axis; thus, PA = y₁ and OA = x₁
• QB is perpendicular from Q to x-axis; thus, QB = y₂ and OB = x₂

This forms two right-angled triangles from the origin to the points, with PA and QB representing vertical distances from the x-axis.

Constructing a Right Triangle

Now consider triangle PQR, where a line segment is drawn from P to Q.

• Draw a horizontal line from P and a vertical line from Q.
• They intersect at point R, forming a right triangle PQR.
• The base (horizontal leg) of the triangle is the horizontal distance: ( |x₂ - x₁| )
• The height (vertical leg) is the vertical distance: ( |y₂ - y₁| )

Using the Pythagorean Theorem

According to the Pythagorean Theorem:

\[ Distance PQ = \sqrt{(x₂ - x₁)^2 + (y₂ - y₁)^2} \]

This construction, using perpendiculars to the x-axis from points P and Q, helps us clearly see that the difference in x-values gives the horizontal side and the difference in y-values gives the vertical side of a right triangle. Applying the Pythagorean theorem gives us the distance formula between any two points in a plane.