Formula for internal division

Internal Division of a Line Segment: Formula and Geometric Interpretation

Assume that the points A(x₁, y₁) and B(x₂, y₂) are the endpoints of a line segment AB. A point P(x, y) lies on the segment AB and divides it internally in the ratio m : n.

Geometrical Construction:

• Drop a perpendicular from point A to meet the x-axis at point L.
• Draw a perpendicular from point B down to the x-axis and mark the foot as point M.
• From point P, draw a perpendicular PN to the x-axis.
• From point A, draw a perpendicular AH to line PN (i.e., vertical line through P).
• From point P, draw a perpendicular PG to BM (i.e., vertical line through B).
• ∠H = 90°, ∠G = 90° — these angles indicate right-angled triangles formed in the figure.

Using Similar Triangles:

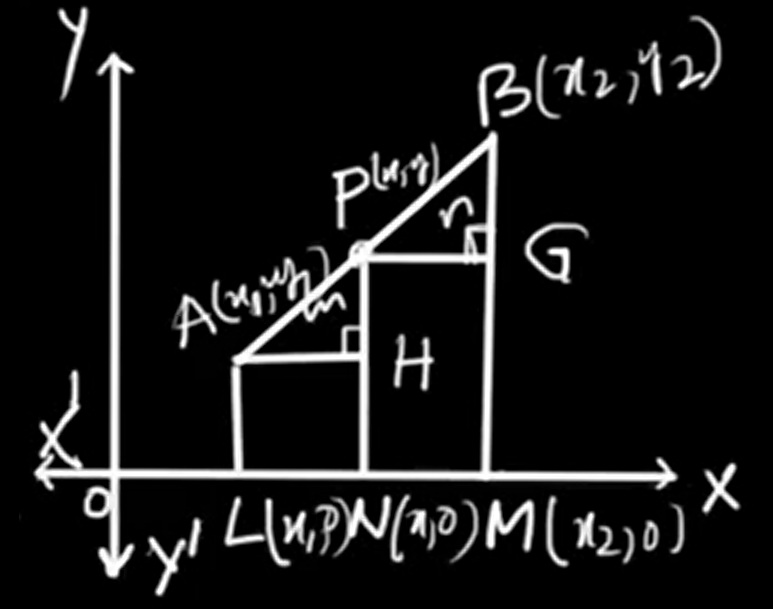
Based on the construction, triangles APH and PBG are similar by AA (Angle-Angle) criterion, as both contain a right angle and the common angle ∠APB.

Using the property of similar triangles:

AH / PG = AP / PB
⟹ AH / PG = m / n

Coordinates from Geometry:

• AH = y − y₁, representing the vertical distance from point A up to point P.
• PG = y₂ − y, which gives the vertical distance from point P down to point B.

Substitute in the ratio:

(y − y₁)/(y₂ − y) = m/n

Cross-multiplying:

n(y − y₁) = m(y₂ − y)

Now solve for y:

n(y) − n(y₁) = m(y₂) − m(y)
⇒ ny + my = m(y₂) + n(y₁)
⇒ y(n + m) = m(y₂) + n(y₁)
⇒ y = (m·y₂ + n·y₁) / (m + n)
  

Similarly, for x-coordinate:

• Use similar triangles formed by horizontal distances (projection on x-axis):
• AN = x − x₁, NG = x₂ − x

(x − x₁)/(x₂ − x) = m/n

Following the same algebraic steps:

n(x − x₁) = m(x₂ − x)
⇒ nx + mx = m(x₂) + n(x₁)
⇒ x(m + n) = m·x₂ + n·x₁
⇒ x = (m·x₂ + n·x₁) / (m + n)
  

Final Coordinates of Point P:

P(x, y) = ( (m·x₂ + n·x₁) / (m + n), (m·y₂ + n·y₁) / (m + n) )

Example:

Let A(2, 3) and B(6, 7), and P divides AB in the ratio 1:2.

x = (1×6 + 2×2) / (1+2) = (6 + 4) / 3 = 10/3 ≈ 3.33
y = (1×7 + 2×3) / (1+2) = (7 + 6) / 3 = 13/3 ≈ 4.33

Therefore, P ≈ (3.33, 4.33)