In this lesson, we explore the scalar triple product through its geometric interpretation. Consider the diagram above. Imagine three vectors \(\vec{a}\), \(\vec{b}\), and \(\vec{c}\) all originating from a common point \(O\). These vectors define the edges of a solid called a parallelepiped.
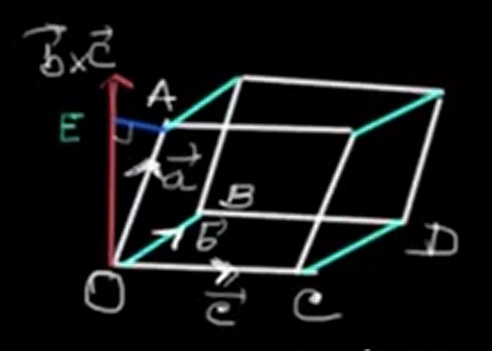
A parallelepiped resembles a skewed box, where none of the angles are necessarily 90°, and opposite faces are parallelograms. The base of this solid can be formed by the parallelogram spanned by vectors \(\vec{b}\) and \(\vec{c}\). The area of this base is given by the magnitude of their cross product:
\[ Area\; of\; parallelogram\; OCDB = |\vec{b} \times \vec{c}| \]
\[ From\; \triangle OAE\; where\; \angle AOE= \theta \; and \; \angle AEO=90° [\because\; AE \perp OE] \] \[We\; get\; |\overrightarrow{a}|\cos\theta= OA \cos \theta = OE = height\; of\; the\; parallelepiped \]
To calculate the volume of the parallelepiped, we multiply the base area by the height. The height is the component of a along the direction of \((\vec{b} \times \vec{c})\), which is perpendicular to the base formed by \(\vec{b}\) and \(\vec{c}\).
\[ \vec{a}.(\vec{b} \times \vec{c})=|\vec{a}| \cos\theta \cdot |\vec{b} \times \vec{c}| \] \[=|b \times c| |a| \cos\theta \] \[ =Area\; of\; the\; OCDB \times height\; of\; the\; parallelepiped \] \[ = Volume\; of\; the\; parallelepiped \]
Combining these, we arrive at the scalar triple product:
\[ \vec{a} \cdot (\vec{b} \times \vec{c}) = Volume\; of\; the\; Parallelepiped \]
A key result derived from this concept is the condition for three vectors to be coplanar. If the volume of the parallelepiped formed by the vectors is zero, then the vectors lie in the same plane.
\[ \vec{a} \cdot (\vec{b} \times \vec{c}) = 0 \Rightarrow \vec{a}, \vec{b}, \vec{c}\; are\; coplanar \]
This result is widely used in vector algebra and geometry, particularly for verifying whether three vectors are coplanar.