The mathematical definition of the modulus function is f(x) = |x|.
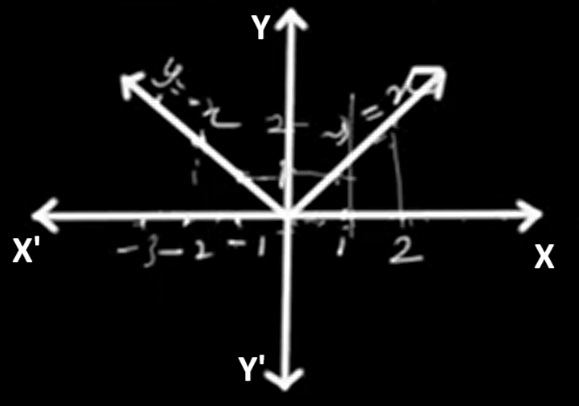
The graph of f(x) = |x| is V-shaped and symmetric about the y-axis. It coincides with the line y = x when x is positive or zero, and with y = -x when x is negative.
The modulus function is defined for every real number: Domain: (-∞, ∞).
The function outputs only non-negative values: Range: [0, ∞).
The greatest integer function, also known as the floor function, is defined as: f(x) = ⌊x⌋. It outputs the largest integer that does not exceed the input value.
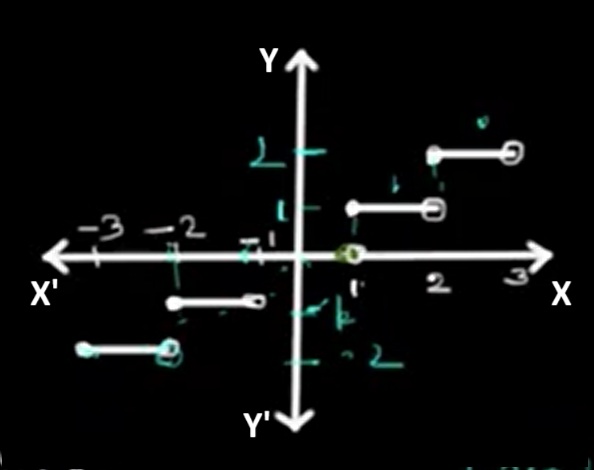
The graph of f(x) = ⌊x⌋ is a step function. The graph features horizontal segments that descend at each integer, forming a step-like pattern. Each interval is left-closed and right-open, with the function taking on the integer value at each step.
You can input any real number into this function: Domain: (-∞, ∞).
All integer values are part of the function's range: Range: {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Facebook
Twitter
Linkedin