Graphical representation of sine, cosine and tangent function

1. Exploring the Graph of f(x) = sin(x)

The sine function outputs the y-coordinate of a point on the unit circle corresponding to a given angle. It is defined as f(x) = sin(x).

Graph Overview:

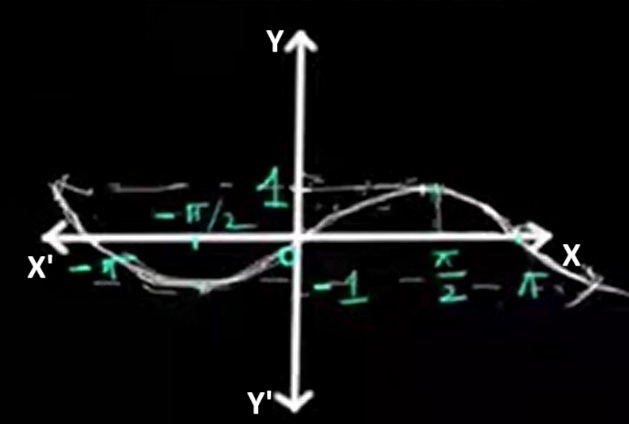
The sine graph is a smooth, continuous wave that oscillates between -1 and 1. It starts at the origin (0,0), rises to 1 at π/2, returns to 0 at π, goes to -1 at 3π/2, and completes one full cycle at 2π.

Domain:

Sine is a continuous function that accepts all real values as input. Domain: (-∞, ∞)

Range:

The cosine function only produces values from -1 to 1. Range: [-1, 1]

Key Characteristics:

• Period: 2π
• Amplitude: 1
• Repeats in a wave pattern

2. Cosine Function: f(x) = cos(x)

The cosine function gives the x-coordinate of a point on the unit circle at a given angle. It is written as f(x) = cos(x).

Graph Overview:

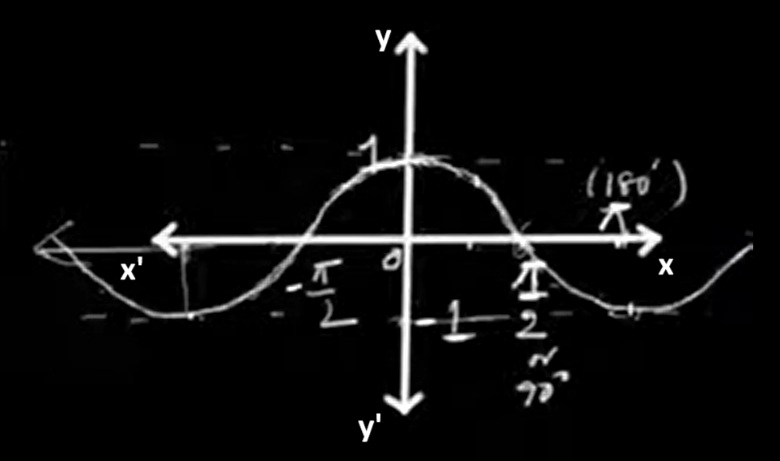
Like the sine graph, the cosine graph is also wave-like and oscillates between -1 and 1. However, it starts at its maximum value, 1, at x = 0. It reaches 0 at π/2, -1 at π, back to 0 at 3π/2, and returns to 1 at 2π.

Domain:

The cosine function has a domain that includes all real values. Domain: (-∞, ∞)

Range:

The values range between -1 and 1. Range: [-1, 1]

Key Characteristics:

• Period: 2π
• Amplitude: 1
• Starts at its peak (x = 0, y = 1)

3. Tangent Function: f(x) = tan(x)

The tangent function is the ratio of sine to cosine: f(x) = tan(x) = sin(x) / cos(x). It measures the slope of the angle's terminal side on the unit circle.

Graph Overview:

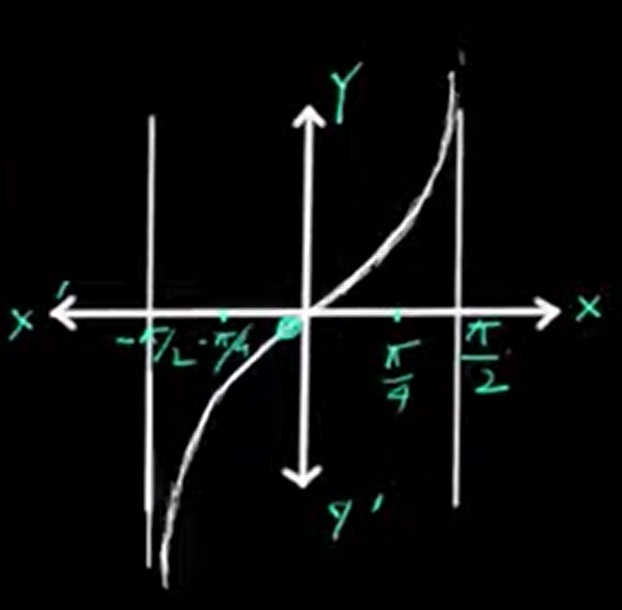
The graph of the tangent function includes vertical asymptotes that occur repeatedly wherever the cosine value equals zero, such as at odd multiples of π/2. It increases steeply between these asymptotes and has no maximum or minimum value.

Domain:

The tangent function is undefined at x = ±π/2, ±3π/2, etc. Domain: x ≠ (2n+1)π/2, where n is an integer

Range:

Unlike sine and cosine, the tangent function can take any real value. Range: (-∞, ∞)

Key Characteristics:

• Period: π
• No amplitude (unbounded)
• Has vertical asymptotes wherever x equals an odd multiple of π/2

Conclusion

Understanding the graphical behavior of sine, cosine, and tangent functions is essential in trigonometry. While sine and cosine show smooth, periodic waveforms with a limited range, the tangent graph behaves differently with steep curves and vertical asymptotes. Recognizing these patterns helps in analyzing trigonometric relationships and solving equations more effectively.