Graphical representation of squared root and reciprocal functions

Eleven Standard >> Graphical representation of squared root and reciprocal functions

Graph of Square Root Function and Reciprocal Function, Their Domain and Range

1. Square Root Function

The square root function is defined as: f(x) = √x.

Graph Description:

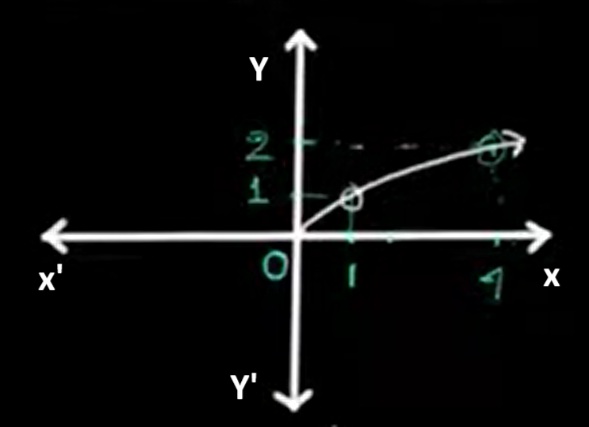
Square root function

The graph of f(x) = √x begins at the point (0, 0) and rises gradually as x increases. It is a curve that lies entirely in the first quadrant.

Domain:

The square root function is defined only for non-negative real inputs: x ≥ 0 or [0, ∞).

Range:

Its output values are limited to non-negative real numbers only: f(x) ≥ 0 or [0, ∞).

Key Points:

f(0) = 0
f(1) = 1
f(4) = 2
f(9) = 3

2. Reciprocal Function

The reciprocal function is defined as: f(x) = 1/x.

Graph Description:

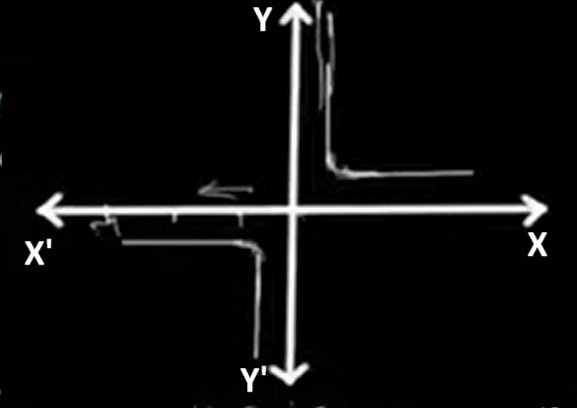
Reciprocal Function

The graph of f(x) = 1/x is a hyperbola with two branches, one in the first quadrant and one in the third. The graph approaches the x-axis and y-axis but never crosses them, as they act as asymptotes.

Domain:

The domain includes all real numbers except 0: x ≠ 0 or (-∞, 0) ∪ (0, ∞).

Range:

The range also excludes 0: f(x) ≠ 0 or (-∞, 0) ∪ (0, ∞).

Key Points:

f(1) = 1
f(2) = 0.5
f(-1) = -1
f(-2) = -0.5

Graphical representation of squared root and reciprocal functions

Eleven Standard >> Graphical representation of squared root and reciprocal functions

Graph of Square Root Function and Reciprocal Function, Their Domain and Range

1. Square Root Function

Graph Description:

Domain:

Range:

Key Points:

2. Reciprocal Function

Graph Description:

Domain:

Range:

Key Points:

You may like this videos