Introduction of Function as a relation

Introduction to Function as a Relation

A function is a unique kind of relation where each input corresponds to exactly one output. Mathematically, a function from set A to set B establishes a unique association between each element of A and an element of B.

Function notation: f: A → B indicates that the function f assigns each element from the domain A to a corresponding element in the codomain B.

Function as a Relation

In terms of relations, a function is considered a subset of the Cartesian product A × B, where each x in set A is associated with exactly one y in set B. The ordered pair (x, y) must exist in the function’s definition for it to be valid.

Example: Consider the function

f = {(x₁, y₂), (x₂, y₁), (x₃, y₃)}

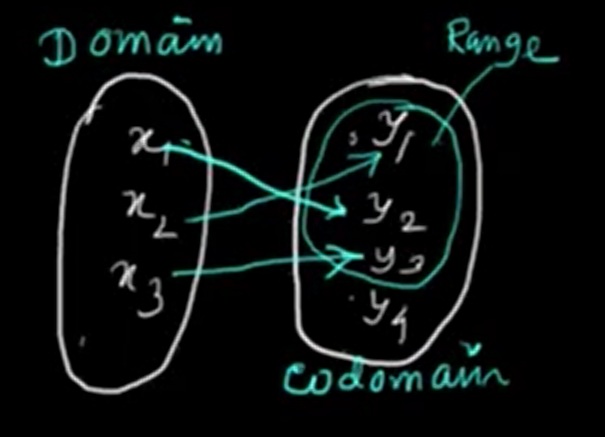
Here, each input x₁, x₂, x₃ is assigned to a unique output in B. Hence, this relation is a function.

Main Features of a Function

• Clearly defined assignment: Each input from the domain is paired with one and only one output in the codomain.
• Unique outputs: No input can be mapped to more than one output.
• Ordered pairs: A function is often represented as a set of ordered pairs (x, y).
• Notation: If f(x) = y, then x is the input and y is the corresponding output.

Domain and Range of a Function

Domain: The set of all input values x for which the function is defined.

Range: The set of all output values y that the function produces when applied to inputs from the domain.

From the example f = {(x₁, y₂), (x₂, y₁), (x₃, y₃)}:

• Domain = {x₁, x₂, x₃}
• Range = {y₁, y₂, y₃}

• A function is a special relation where each input maps to exactly one output.
• Functions can be represented using set notation, mappings, or graphs.
• The domain and range help us understand what inputs a function accepts and what outputs it produces.