Operations on set | Part -1

Operations on Sets

Set operations are fundamental concepts in mathematics used to combine, compare, or relate different sets. The most common operations include union, intersection, and difference.

1. Union of Two Sets

The union of two sets consists of every element that appears in at least one of the sets. It is denoted by the symbol ∪.

Definition: Given two sets A and B, the union is expressed as:

A ∪ B = { x | x ∈ A or x ∈ B }

Example:

Let A = {1, 3, 5} and B = {2, 3, 5, 7}

Then, A ∪ B = {1, 2, 3, 5, 7}

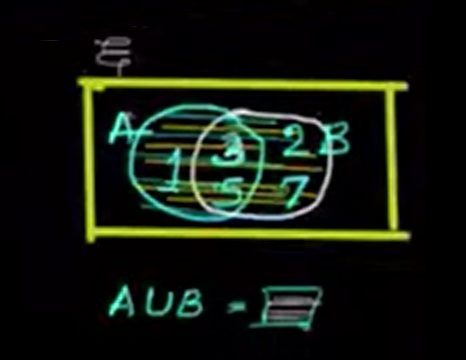
Note: Duplicates are not included in sets, so repeated elements appear only once.

2. Intersection of Two Sets

The intersection of two sets includes only those elements that are common to both sets. It is denoted by the symbol ∩.

Definition: For any two sets A and B, their intersection is written as:

A ∩ B = { x | x ∈ A and x ∈ B }

Example:

Let A = {1, 4, 7} and B = {1, 3, 4, 5}

Then, A ∩ B = {1, 4}

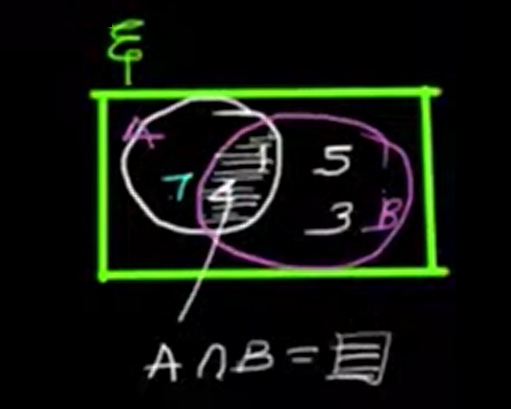
Only the elements that appear in both sets A and B are included in the result.

Understanding set operations like union and intersection is essential in various areas of mathematics and computer science. These operations allow us to manipulate and analyze data, model relationships, and solve problems effectively.