Operations on set | Part -2

Operations on Sets: Difference, Symmetric Difference, and Complement

Set theory provides a variety of operations that allow us to compare and manipulate sets. In addition to union and intersection, three other key operations in set theory include the difference, symmetric difference, and complement. These operations are useful for identifying unique elements, contrasting sets, and understanding relationships within a universal context.

1. Difference of Two Sets

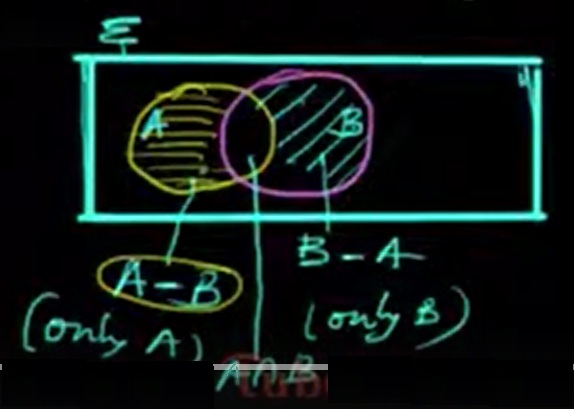
The difference between two sets, written as A − B, includes all elements that are in set A but not in set B.

Definition: A − B = { x | x ∈ A and x ∉ B }

Example:

Let A = {1, 2, 5, 7} and B = {3, 4, 5, 6, 7}

Then A − B = {1, 2}

Only the elements 1 and 2 are in A but not in B.

2. Symmetric Difference of Two Sets

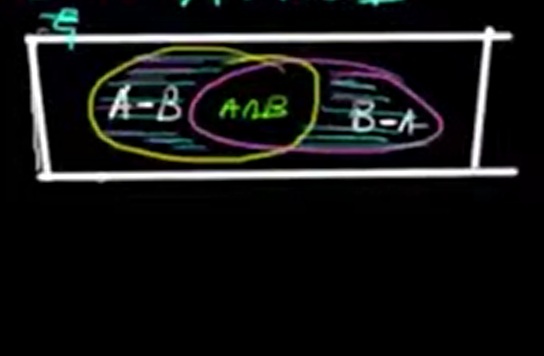
The symmetric difference between two sets consists of elements that belong to one set or the other, but not to both. It is typically represented by the symbol Δ or occasionally ⊕.

Definition: A Δ B = (A − B) ∪ (B − A)

Example:

Using the same sets: A = {1, 2, 5, 7} B = {3, 4, 5, 6, 7}

A − B = {1, 2} and B − A = {3, 4, 6}

So, A Δ B = {1, 2, 3, 4, 6}

The elements 5 and 7 appear in both sets and are excluded from the symmetric difference.

3. Complement of a Set

The complement of a set A (written as A′ or A^c) consists of all elements in the universal set that are not in A.

Definition: A′ = { x | x ∈ U and x ∉ A }

Here, U represents the universal set, which must be defined beforehand.

Example:

Let the universal set U = {1, 2, 3, 4, 5, 6, 7, 8} and A = {1, 2, 4, 6}

Then A′ = {3, 5, 7, 8}

These are the elements in the universal set that do not belong to A.

Set operations like difference, symmetric difference, and complement are powerful tools in mathematics that help us identify distinctions between sets and describe what is excluded or uniquely present. Mastering these concepts is essential for deeper studies in algebra, logic, and computer science.