Polar representation of complex numbers on argand diagram

Geometrical Interpretation of Complex Numbers on the Argand Diagram

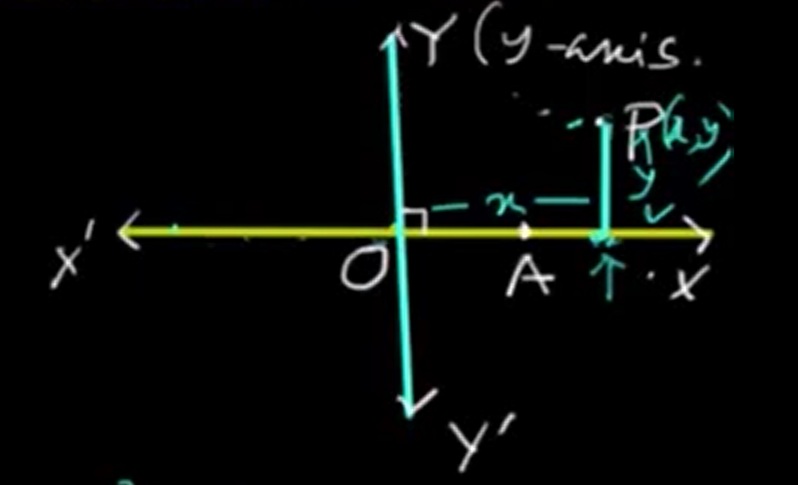
A complex number \( z = x + iy \), where \( x \) and \( y \) are real numbers, can be represented as a point \( P(x, y) \) on the Argand diagram, which is essentially the Cartesian coordinate system used for complex numbers. Take a point A on XOX' such that OA=1 unit.

In this diagram:

• \( \overline{OA} = x \) (along the real axis)
• \( \overline{AP} = y \) (along the imaginary axis)
• \( \overline{OP} \) is the line (or modulus) connecting the origin \( O(0,0) \) to the point \( P(x, y) \)

Let \( z = x + iy \). Let's analyze specific cases:

• If \( y = 0 \), then \( z = x + 0i = x \Rightarrow z = Re(z) \). All such numbers lie on the real axis (x-axis or \( X'OX \)). This axis is also referred to as the real axis.
• If \( x = 0 \), then \( z = 0 + iy = iy \), which is a purely imaginary number. All such numbers lie on the imaginary axis (y-axis or \( Y'OY \)). This axis is called the imaginary axis.

Therefore:

• Every real number corresponds to a point on the x-axis (real axis)
• Every purely imaginary number corresponds to a point on the y-axis (imaginary axis)

Any point \( P(x, y) \) in this plane (called the complex plane or Argand plane) represents a complex number. The distance \( OP \), denoted as \( |z| \), is the modulus of the complex number.

The angle \( \theta \) made by \( OP \) with the positive real axis is called the argument of the complex number, denoted \( \arg(z) \).

Thus, the complex number \( z = x + iy \) can also be expressed in polar form as:

\( z = r(\cos \theta + i \sin \theta) = r cis \theta \)

where:

• \( r = |z| = \sqrt{x^2 + y^2} \)
• \( \theta = \tan^{-1}(\frac{y}{x}) \)