Practical problems on set | Part-2

Set Operations Involving Three Finite Sets and a Universal Set

When we are dealing with three finite sets, A, B, and C, within a universal set denoted by ξ (or U), we can analyze their relationships using fundamental set operations such as union, intersection, and complement.

1. Universal Set (ξ or U)

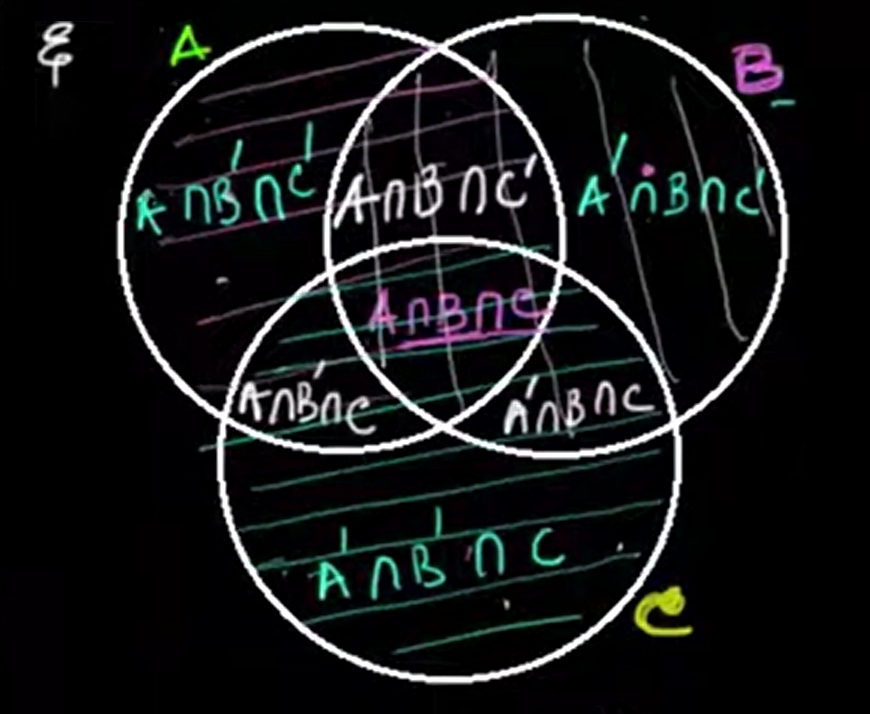
The universal set ξ includes all elements under consideration. Every element of sets A, B, and C must be a member of ξ.

2. Union of Three Sets

A ∪ B ∪ C includes all elements that are in A, B, or C (or in more than one of them).

3. Intersection of Three Sets

A ∩ B ∩ C represents the set of elements that are shared by all three sets A, B, and C.

4. Complement of a Set

The complement of A (denoted A′ or A^c) includes all elements in ξ that are not in A.

5. De Morgan's Rules in the Context of Three Sets

De Morgan's Laws help in simplifying expressions involving complements:

• (A ∪ B ∪ C)′ = A′ ∩ B′ ∩ C′
• (A ∩ B ∩ C)′ = A′ ∪ B′ ∪ C′

6. Cardinality in Three Sets

The total count of elements in A ∪ B ∪ C can be determined using the following formula:

|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B ∩ C|

7. Venn Diagram

For three sets, a Venn diagram has 8 distinct regions representing all possible intersections and exclusions. These are:

• Only A
• Only B
• Only C
• A ∩ B only
• A ∩ C only
• B ∩ C only
• A ∩ B ∩ C
• None (outside all three sets, but still within ξ)

Grasping how three sets interact within a universal set is essential for tackling advanced problems in areas such as set theory, logic, probability, and data interpretation.