Ratios of angle in (- theta) in terms of (theta)

Trigonometric Ratios for Negative Angles Using Reflected Points

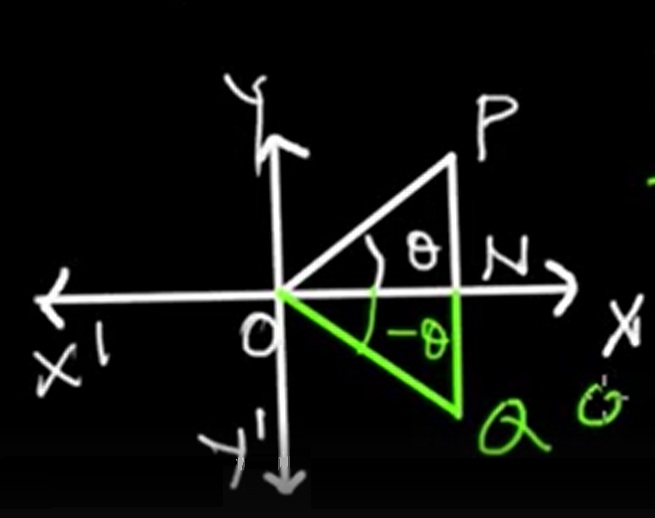
Let O be the origin, and P(x, y) be a point in the first quadrant such that the line segment OP makes an angle θ with the positive x-axis.

Now, reflect point P across the x-axis to get a new point Q(x, -y). The mirrored point is positioned in the fourth quadrant, where the segment OQ creates an angle of −θ relative to the x-axis.

Let the distance from the origin to the point (the hypotenuse) be denoted as r, where:
r = √(x² + y²)

By applying coordinate geometry and fundamental trigonometric ratios, we can deduce the following identities:

• Sine:
  sin(θ) = y / r
  sin(–θ) = –y / r = –sin(θ)
• Cosine:
  cos(θ) = x / r
  cos(–θ) = x / r = cos(θ)
• Tangent:
  tan(θ) = y / x
  tan(–θ) = –y / x = –tan(θ)
• Cosecant:
  csc(θ) = 1 / sin(θ) = r / y
  csc(–θ) = 1 / sin(–θ) = r / (–y) = –csc(θ)
• Secant:
  sec(θ) = 1 / cos(θ) = r / x
  sec(–θ) = 1 / cos(–θ) = r / x = sec(θ)
• Cotangent:
  cot(θ) = x / y
  cot(–θ) = x / (–y) = –cot(θ)

Therefore, trigonometric functions with odd symmetry—such as sine, tangent, cosecant, and cotangent—reverse their signs for negative angles, whereas even functions like cosine and secant retain their original values.