Representation of fractional part and signum functions with graph

1. Exploring the Fractional Part Function: f(x) = {x}

The fractional part function, denoted as f(x) = {x}, returns the non-integer part of a real number. Mathematically, it is expressed as: {x} = x - ⌊x⌋, where ⌊x⌋ is the greatest integer less than or equal to x.

Graph Overview:

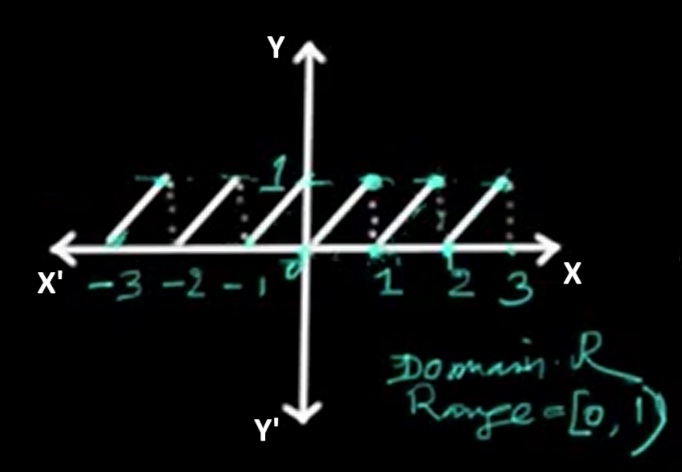
The fractional part function graph is made up of repeating straight-line segments from 0 to just below 1. Each segment starts from 0 (excluded) and increases linearly to just below 1 (included), then drops back to 0 at the next integer.

Domain:

The function accepts any real number as input. Domain: (-∞, ∞)

Range:

Its range is the half-open interval [0, 1), meaning it includes 0 but excludes 1. Range: [0, 1)

Key Features:

• Periodic with period 1
• The function has breaks at whole number values
• Each interval (n, n+1) forms a straight line from 0 to just below 1

2. Signum Function: f(x) = sgn(x)

The signum function, written as f(x) = sgn(x), returns the sign of a real number. Its definition is as follows:

• f(x) = 1 if x > 0
• f(x) = 0 if x = 0
• f(x) = -1 if x < 0

Graph Overview:

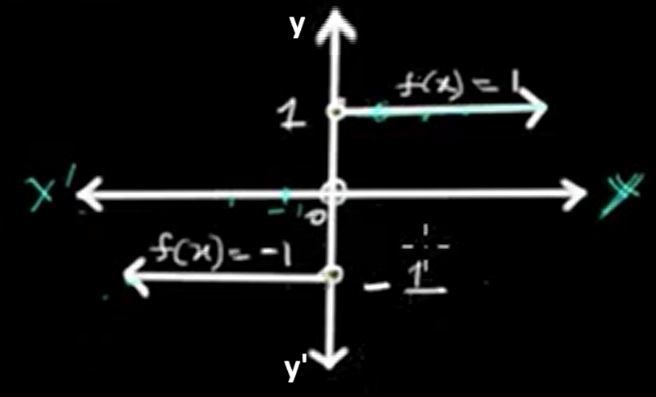
The graph of the signum function consists of three distinct constant segments: It forms a flat line at y = -1 when x is negative, includes the point (0, 0), and creates another flat line at y = 1 for positive x-values.

Domain:

The function is defined for all real numbers. Domain: (-∞, ∞)

Range:

The output is limited to three values only: -1, 0, and 1. The set of outputs is {-1, 0, 1}

Key Features:

• Shows the direction of x (negative, zero, or positive)
• Discontinuous at x = 0
• Commonly used in piecewise and control logic functions

The fractional part and signum functions each serve specific purposes in mathematics. The fractional part function isolates the decimal portion of a number, while the signum function identifies the sign of a value. Their graphs help visualize these behaviors clearly—especially the periodic nature of {x} and the step-like behavior of sgn(x).