Slope or gradient of a straight line

Slope or Gradient of a Straight Line

The slope or gradient of a straight line is a measure of its steepness. It indicates how steeply the line ascends or descends when moving from left to right. Mathematically, if a line makes an angle θ with the positive direction of the x-axis, then the slope of the line is defined as:

m = tan(θ)

1. Finding the Slope Using Two Points

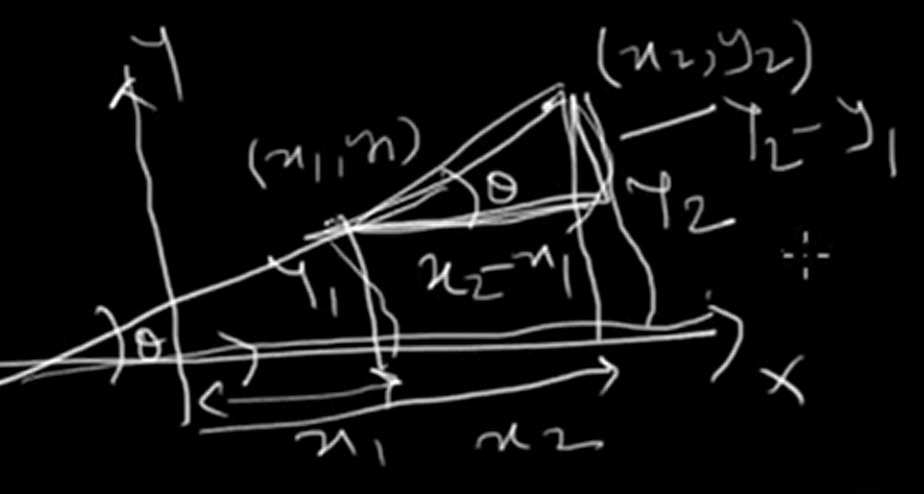
Suppose a straight line passes through two points P(x₁, y₁) and Q(x₂, y₂). To determine the slope, follow this geometric approach:

• Construct a perpendicular line from point P down to meet the x-axis at point A. The length of OA (distance from origin to foot of perpendicular) is x₁.
• From point Q, draw a perpendicular QB to the x-axis. The length of OB is x₂.
• The vertical length between P and Q is the difference in y-coordinates: y₂ − y₁.
• The horizontal length between P and Q is x₂ − x₁.

These points and lines form a right triangle, with the slope line as the hypotenuse. By using the definition of tangent (opposite/adjacent) in right triangles:

m = tan(θ) = (y₂ − y₁) / (x₂ − x₁)

2. Special Cases

• Line Parallel to X-axis: If y₂ = y₁, then the slope m = 0. The line is horizontal.
• Vertical Line (Y-axis Parallel): If both x-values are the same, i.e., x₂ = x₁, the line is vertical and has an undefined slope.

3. Positive vs Negative Slope

• A positive slope occurs when y₂ − y₁ > 0 and x₂ − x₁ > 0, meaning the line goes upward as it progresses from left to right.
• If y₂ − y₁ < 0 and x₂ − x₁ > 0, the slope is negative. The line falls from left to right.

4. Visualization

This concept is often illustrated using two perpendiculars from each point to the x-axis. The difference in y-values gives the vertical change, and the difference in x-values gives the horizontal change. Together, they form a right triangle where the slope is the tangent of the angle the line makes with the x-axis.

The slope is a fundamental property of straight lines and plays an important role in coordinate geometry, helping to classify and understand the orientation and behavior of lines.