Vector algebra in two dimensional plane

Vector Algebra in Two-Dimensional Plane

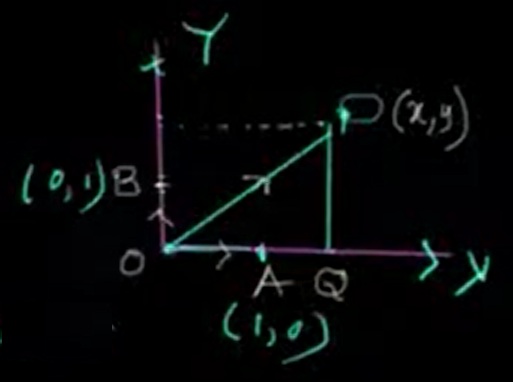
Let us take two points: A\(1, 0\), which is positioned on the x-axis, and B\(0, 1\), located on the y-axis. The origin O is at \(0, 0\).

• The length of OA is 1 unit, and the vector is \(\vec{OA} = \hat{i}\).
• The length of OB is 1 unit, and the vector is \(\vec{OB} = \hat{j}\).

Let P\(x, y\) be any point on the XY-plane. Begin at the origin O and draw a horizontal vector \(\vec{OQ} = x\hat{i}\). From point Q, extend a vertical vector \(\vec{QP} = y\hat{j}\) upward to reach point P.

Thus, the position vector of point P from the origin is:

\(\vec{r} = \vec{OP} = \vec{OQ} + \vec{QP} = x\hat{i} + y\hat{j}\)

This vector \(\vec{r}\) has two components:

• \(x\hat{i}\): the component along x-axis
• \(y\hat{j}\): the component along y-axis

For example, if P\(2, 3\), then \(\vec{OP} = 2\hat{i} + 3\hat{j}\)

Theorem:

Any vector \(\vec{a}\) in a two-dimensional plane can be expressed as:

\(\vec{a} = x\hat{i} + y\hat{j}\)

Here, \(\hat{i}\) and \(\hat{j}\) are unit vectors along the X and Y axes respectively. These unit vectors are mutually perpendicular, and the vector \(\vec{a}\) lies in the plane formed by them (i.e., it is coplanar with \(\hat{i}\) and \(\hat{j}\)).

Magnitude of \(\vec{r}\)

The magnitude (length) of the position vector \(\vec{r} = x\hat{i} + y\hat{j}\) is given by:

\(|\vec{r}| = \sqrt{x^2 + y^2}\)

Unit Vector \(\hat{r}\) along \(\vec{OP}\)

The unit vector along \(\vec{OP}\) is:

\(\hat{r} = \frac{\vec{r}}{|\vec{r}|} = \frac{x\hat{i} + y\hat{j}}{\sqrt{x^2 + y^2}} = \frac{x}{|\vec{r}|}\hat{i} + \frac{y}{|\vec{r}|}\hat{j}\)

Direction Cosines

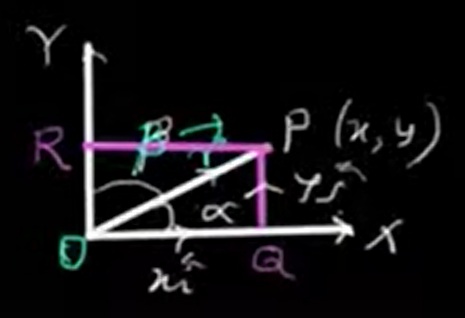
Let angle \(\alpha\) be the angle between \(\vec{r}\) and the x-axis (angle POX), and let \(\beta\) be the angle between \(\vec{r}\) and the y-axis (angle RPO), where R is the foot of perpendicular from P to the y-axis.

Then,

• \(\cos\alpha = \frac{OQ}{OP} = \frac{x}{|\vec{r}|} = l\)
• \(\cos\beta = \frac{OR}{OP} = \frac{y}{|\vec{r}|} = m\)

Hence, the unit vector \(\hat{r}\) can also be written as:\)

\(\hat{r} = \cos\alpha\hat{i} + \cos\beta\hat{j} = l\hat{i} + m\hat{j}\)

Relation Between Direction Cosines

\(l^2 + m^2 = \left(\frac{x^2}{x^2 + y^2}\right) + \left(\frac{y^2}{x^2 + y^2}\right) = \frac{x^2 + y^2}{x^2 + y^2} = 1\)

Here, \(l\) and \(m\) are called the direction cosines of the vector, while \(x\) and \(y\) are called the direction ratios.