Vector in three dimensions | Part -1

Vectors in 3 Dimensions

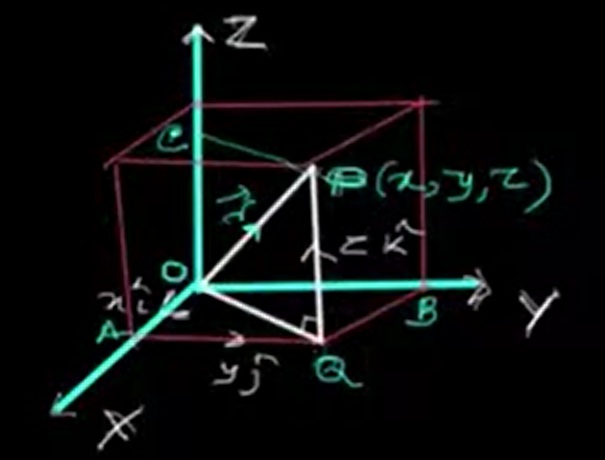
In three-dimensional space, every point is represented using three coordinates: x, y, and z. A vector from the origin O(0, 0, 0) to a point P(x, y, z) in 3D space is called a position vector.

Unit Vectors: \(\hat{i}, \hat{j}, \hat{k}\)

To describe a vector in 3D, we use three mutually perpendicular unit vectors:

• \(\hat{i}\) – unit vector along the x-axis
• \(\hat{j}\) – unit vector along the y-axis
• \(\hat{k}\) – unit vector along the z-axis

Vector Representation in 3D

Any vector \(\vec{v}(x, y, z)\) can be written as a linear combination of the unit vectors:

\(\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}\)

This means the vector from the origin to the point P can be broken down into three components:

• \(\vec{OA} = x\hat{i}\) – along the x-axis
• \(\vec{AQ} = y\hat{j}\) – parallel to the y-axis
• \(\vec{QP} = z\hat{k}\) – vertical rise along the z-axis

Hence, the total displacement vector from the origin O to the point P is:

\(\vec{OP} = \vec{OA} + \vec{AQ} + \vec{QP} = x\hat{i} + y\hat{j} + z\hat{k}\)

Magnitude of a 3D Vector

The length or magnitude of vector \(\vec{v} = x\hat{i} + y\hat{j} + z\hat{k}\) is given by:

\(|\vec{v}| = \sqrt{x^2 + y^2 + z^2}\)

Conclusion

Vectors in 3D are an essential part of geometry and physics, allowing us to describe directions and magnitudes in space using the standard unit vectors \(\hat{i}, \hat{j}, \hat{k}\). Decomposing vectors into these components provides an intuitive way to visualize and compute with them in three-dimensional space.